Solve roots for 4x4 matrix in proof of Proposition 2.2:

(*  * H = RE (H) is a symmetric matrix *)H = {{H11, H12, H13}, {H12, H ... vector *)p = {p1, p2, p3} ; H // MatrixFormM // MatrixForm

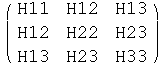
( H11 H12 H13 ) H12 H22 H23 H13 H23 H33

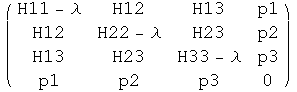
( H11 - λ H12 H13 p1 ) H12 ... H23 H33 - λ p3 p1 p2 p3 0

(* Calculate LHS of equation *)detM = FullSimplify[Det[M]] ; Collect[%, λ]

H23^2 p1^2 - H22 H33 p1^2 - 2 H13 H23 p1 p2 + 2 H12 H33 p1 p2 + H13^2 p2^2 - H11 H33 p2^2 + 2 ... + H33 p2^2 - 2 H13 p1 p3 - 2 H23 p2 p3 + (H11 + H22) p3^2) λ + (-p1^2 - p2^2 - p3^2) λ^2

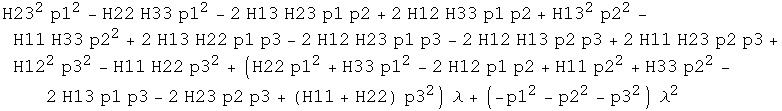
(*  * define adjugate of H*)adH = Inverse[H] Det[H] ; adH // MatrixForm

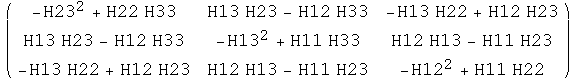
( 2 ) -H2 ... 2 -H13 H22 + H12 H23 H12 H13 - H11 H23 -H12 + H11 H22

FullSimplify[detM -  (-p . p λ^2 - p . (H - Tr[H] IdentityMatrix[3]) . p λ - p . adH . p) ]

0

We have shown that
    det 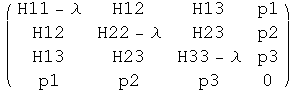( H11 - λ H12 H13 p1 ) H12 ... H23 H33 - λ p3 p1 p2 p3 0= A λ^2 + B λ + C
where
    A = -p.p
    B = -p . (H - Tr[H] IdentityMatrix[3]) . p
    C = - p . adH . p
    

Viete's formulas

rts = Solve[A x^2 + B x + C0, x]

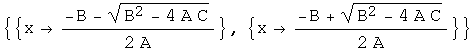
{{x (-B - (B^2 - 4 A C)^(1/2))/(2 A)}, {x (-B + (B^2 - 4 A C)^(1/2))/(2 A)}}

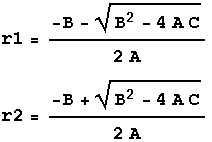
r1 = (-B - (B^2 - 4 A C)^(1/2))/(2 A) r2 = (-B + (B^2 - 4 A C)^(1/2))/(2 A)

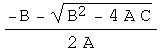
(-B - (B^2 - 4 A C)^(1/2))/(2 A)

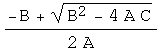
(-B + (B^2 - 4 A C)^(1/2))/(2 A)

FullSimplify[r1 r2]

C/A

FullSimplify[r1 + r2]

-B/A

Print notebook:

Directory[] SetDirectory["notebooks"]

NotebookPrint[SelectedNotebook[], "/home/fdahl/writing/riccati/notebooks/det of 4x4 matrix.nb.ps"]

Created by Mathematica  (March 10, 2006)